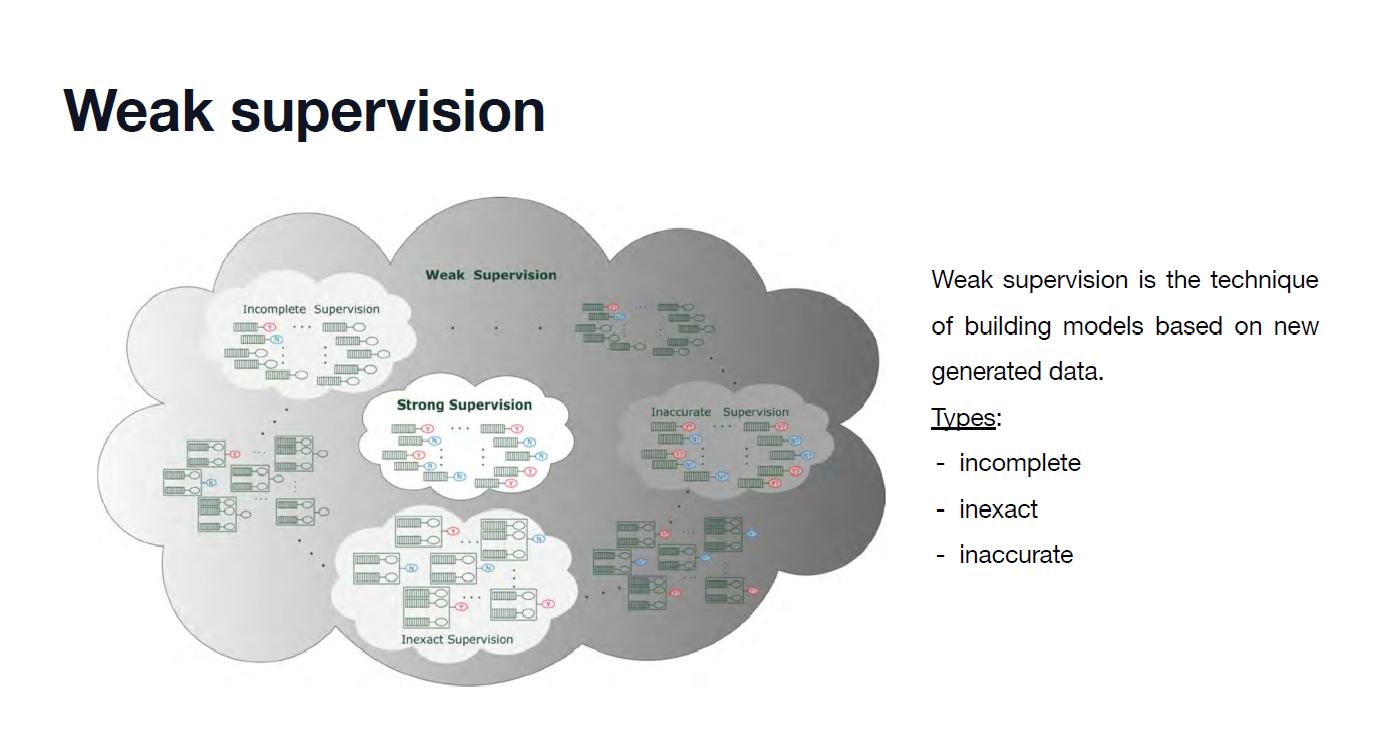
DBMS: Normalization

INTRO 🙌

저번 시간에는 Transaction Management 에 대하여 알아보았다.

이번 시간에는 Normalization에 대해 알아보자.

---

배경지식 🍔

DB Design

Bad Design

[Bad Design]

• Relation may not be well-designed, thus causing us a lot of problems
• Problems(= Anomalies):
  • Redundancy: repetition of data
    • update anomalies
      • update one item and forget others
      • inconsistencies
    • deletion anomalies
      • delete many items
      • delete one item, loose other information
    • insertion anomalies
      • can’t insert one item without inserting others

Good Design

[Better Design: Break the relation into two]

• Original db schema R 사용
• Good design R* 얻을 때까지 반복
• R* 이상적인 조건
  • R 정보 포함
  • Redundancy ↓
  • Dependency-preserving; R \(\leftrightarrow\) constraints C \(\rightarrow\) C \(\leftrightarrow\) R*
  • Good query performance

그렇다면, 어떻게 좋은 R* 찾아낼 수 있을까?

상기 문제를 해결하고자 고안된 것이 바로 normal forms이다.

---

Normal Forms 🍚

• DB gurus:
  • Normal forms (Boyce-Codd, 3rd, and 4th normal forms)
    • Based on various constraints
      • Functional dependencies and keys
    • R* = one of these forms \(\rightarrow\) R* is guaranteed to achieve certain good properties
      • e.g., if R* is in Boyce-Codd NF, it is guaranteed to not have certain types of redundancy
  • Algorithms to transform R into R* that is in some of these normal forms
  • Trade-offs among normal forms
• Our job:
  • learn these forms
  • transform R into R* in one of these forms
  • carefully evaluate the trade-offs

Normalization 목적 ★★★★★★★★★

To find a good relational schema by minimizing redundency

---

Relation Keys

• Key of a relation R is a set of attributes (primary key)
  • functionally determines all attributes of R
    • creates a FD A \(\rightarrow\) B
  • none of its subsets determines all attributes of R
• Superkey \(\Leftrightarrow\) Key
  • a set of attributes that contains a key

Finding the Keys of a Relation

1. Entity set: the key of the relation = the set of attributes, the key of the entity set.

1. Many-many relationship: the key of the relation = the set of all attribute keys in the relations corresponding to the entity sets

1. Many-one, one-many, one-one relationships, Multi-way relationships, Weak entity sets

The set of attributes A is a key \(\rightarrow\) certain FDs are true.

---

Functional Dependencies

\(A \rightarrow B:\ A\ functionally\ determines\ B\)

• A form of constraint (hence, part of the schema)
• Finding them is part of the database design
• Used heavily in schema refinement
• When creating a DB schema, we should list all FDs we believe are valid
• FDs should be valid on ALL DB database instances conforming to our schema

\(A_1,A_2,...,A_n\ \rightarrow\ B_1,B_2,...,B_n\)

• If two tuples agree on the attributes \(A_1,A_2,...,A_n\), then they must also agree on the attributes \(B_1,B_2,...,B_n\)

\[EmpID\ \rightarrow Name,\ Phone,\ Position\] \[Position\ \rightarrow\ Phone\] \[Phone\ \nrightarrow\ Position\]

Phone 1234는 Position에서 Clerk과 Lawyer 두 가지 튜플을 가지기 때문에 dependency가 성립하지 않는 모습이다.

Functional Dependency 증명

[\(A \rightarrow B\)]

1. Erase all other columns
2. Check if \(A\ \Leftrightarrow \ B\) many-one (called functional in mathematics)

Reasoning with FDs

1) closure of FD sets

Relation Schema R: \(R = {A,B,C,G,H,I}\)

A set S of FDs: \(S = A \rightarrow B, A \rightarrow C, CG \rightarrow H, CG \rightarrow I, B \rightarrow H\)

• Closure of S: S+ = all FDs logically implied by S
• \(A \rightarrow H\) logically implied
• Compute S+ using Armstrong’s axioms
  • For each f in S, apply reflexivity and augment. rules
  • Add the new FDs to S+
  • For each pair of FDs in S, apply the transitivity rule
  • Add the new FD to S+
  • Until S+ does not change any further

Armstrong’s Axioms

• Reflexivity rule
  • \[A1A2...An \rightarrow\ a\ subset\ of\ A1A2...An\]
• Augmentation rule
  • \[A1A2...An \rightarrow B1B2...Bm,\ then\ A1A2...An C1C2..Ck \rightarrow B1B2...Bm C1C2...Ck\]
• Transitivity rule
  • \[A1A2...An \rightarrow B1B2...Bm\ and\ B1B2...Bm \rightarrow C1C2...Ck,\ then\ A1A2...An \rightarrow C1C2...Ck\]

Additional Rules

• Union rule
  • \(X \rightarrow Y\ and\ X \rightarrow Z,\ then\ X \rightarrow YZ\) (X, Y, Z are sets of attributes)
• Decomposition rule
  • \[X \rightarrow YZ,\ then\ X \rightarrow Y\ and\ X \rightarrow Z\]
• Pseudo-transitivity rule
  • \[X \rightarrow Y\ and\ YZ \rightarrow U,\ then\ XZ \rightarrow U\]

2) closure of attribute sets

The closure of {A1, …, An}, denoted {A1, …, An}+, is the set of all such attributes B

• 1) Functionally determined by A1, …, An
• 2) Satisfies S, a set of FDs S

---

Desirable Properties of Schema Refinement

1. minimize redundancy
2. avoid info loss (lossless decomposition)
3. preserve dependency
4. ensure good query performance

Relation Decomposition

Desirable Property #1: Minimize redundancy

분해된 테이블들을 다시 기존 테이블로 변환할 때, 하기 문제점이 발생한다.

---

Boyce Codd Normal Form (BCNF)

[BCNF]

A simple condition for removing anomalies from relations:

        Whenever there is a nontrivial FD {A1,A2,...,An --> B}
        for  R , it is the case that {A1,A2,...,An --> B}
        is a super-key for R. 

Super Key

Whenever a set of attributes of R is determining another attribute, it is a super-key, and thus should determine all attributes of R. (A key is also a super-key)

BCNF Decomposition

• BCNF removes certain types of redundancy
• For examples of redundancy that it cannot remove, see “multivalued redundancy”
• BCNF avoids info loss

1. Find a dependency that violates the BCNF condition:

\[A_1, A_2, … A_n \rightarrow B_1, B_2, ..., B_m\]

1. Decompose: Continue until there are no BCNF violations left.

Any 2-attribute relation is in BCNF.

예시 1

What are the FDs?

• \(SSN \rightarrow Name\).

Does this FD satisfy the BCNF condition?

• No, \(SSN \nrightarrow Phone\ Number\).

Is the relation in BCNF?

• No

Decompose it into BCNF

• 주어진 FD에서 \(super\ key \rightarrow 나머지\).
  • \(SSN \rightarrow Phone\ Number\) 추가.

예시 2

FD: \(SSN \rightarrow Name, Age, Eye\ Color\). BCNF: \(Person1(SSN, Name, Age, EyeColor), Person2(SSN, PhoneNumber)\).

예시 3

FD:

• \(SSN \rightarrow Name, Age, Eye\ Color\).
• \(Age \rightarrow Draft-worthy\).

BCNF: \(Person1a(SSN,Name,Age,EyeColor),\ Person1b(Age, Draft-worthy),\ Person2(SSN, PhoneNumber)\)

• STEP 1: \(SSN \rightarrow Name, Age, EyeColor, Draft-worthy\).
  • STEP 2: \(SSN \rightarrow Name, Age, EyeColor\).
  • STEP 2: \(Age \rightarrow Draft-worthy\).
• STEP 1: \(SSN \rightarrow PhoneNumber\).

더 많은 예제

---

Reference

Database Management Systems by Raghu Ramakrishnan and Johannes Gehrke